Saccheri quadrilateral
A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclid vindicatus (1733), an attempt to prove the parallel postulate using the method Reductio ad absurdum. The first known consideration of the Saccheri quadrilateral was by Omar Khayyam in the late 11th century, and it may occasionally be referred to as the Khayyam-Saccheri quadrilateral.[1]
For a Saccheri quadrilateral ABCD, the sides AD and BC (also called legs) are equal in length and perpendicular to the base AB. The top CD is called the summit or upper base and the angles at C and D are called the summit angles.
The advantage of using Saccheri quardrilaterals when considering the parallel postulate is that they place the mutually exclusive options in very clear terms:
- Are the summit angles right angles, obtuse angles, or acute angles?
As it turns out, when the summit angles are right angles, this quadrilateral is equivalent to the statement expounded by Euclid's fifth postulate. When they are acute, this quadrilateral leads to hyperbolic geometry, and when they are obtuse, the quadrilateral leads to elliptical geometry. Saccheri himself, however, thought that both the obtuse and acute cases could be shown to be contradictory.
Contents |
History
Saccheri quadrilaterals were first considered by Omar Khayyam (1048-1131) in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid.[1] Unlike many commentators on Euclid before and after him (including of course Saccheri), Khayyam was not trying to prove the parallel postulate as such but to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle):
- Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge.[2]
Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.
It wasn't until 600 years later that Giordano Vitale made an advance on Khayyam in his book Euclide restituo (1680, 1686), when he used the quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant.
Saccheri himself based the whole of his long, heroic, and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.
A formula
In the hyperbolic plane of constant curvature 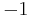 , the summit
, the summit  of a Saccheri quadrilateral can be calculated from the leg
of a Saccheri quadrilateral can be calculated from the leg 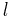 and the base
and the base  using the formula
using the formula
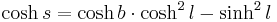 .[3]
.[3]
See also
Notes
- ^ a b Boris Abramovich Rozenfelʹd (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space (Abe Shenitzer translation ed.). Springer. p. 65. ISBN 0387964584. http://books.google.com/books?id=DRLpAFZM7uwC&pg=PA65.
- ^ Boris A Rosenfeld and Adolf P Youschkevitch (1996), Geometry, p.467 in Roshdi Rashed, Régis Morelon (1996), Encyclopedia of the history of Arabic science, Routledge, ISBN 0415124115.
- ^ P. Buser and H. Karcher. Gromov's almost flat manifolds. Asterisque 81 (1981), page 104.
References
- George E. Martin, The Foundations of Geometry and the Non-Euclidean Plane, Springer-Verlag, 1975
- M. J. Greenberg, Euclidean and Non-Euclidean Geometries: Development and History, 4th edition, W. H. Freeman, 2008.